Dua buah vektor atau lebih dapat dijumlahkan atau dikurangi. Ada beberapa cara penjumlahan dan pengurangan vektor.
1. Cara Grafis
Cara ini menekankan pada cara menggambarnya. Yang termasuk dalam cara grafis adalah cara poligon, cara segitiga dan cara jajaran genjang.
a. Cara Poligon
 |
| |||||
| |||||
Ø
|
Ø
|
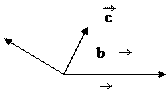
Ø  Gambarkan resultan vektor r yang merupakan jumlah dari vektor a, b dan c dengan cara menggambarkan vektor dari pangkal vektor a ke ujung vektor c, vektor resultan dinyatakan dengan besarnya atau penjang vektor resultan dan arahnya sesuai dengan hasil dari gambar yang didapat, seperti vektor berikut ini
Gambarkan resultan vektor r yang merupakan jumlah dari vektor a, b dan c dengan cara menggambarkan vektor dari pangkal vektor a ke ujung vektor c, vektor resultan dinyatakan dengan besarnya atau penjang vektor resultan dan arahnya sesuai dengan hasil dari gambar yang didapat, seperti vektor berikut ini
 Gambarkan resultan vektor r yang merupakan jumlah dari vektor a, b dan c dengan cara menggambarkan vektor dari pangkal vektor a ke ujung vektor c, vektor resultan dinyatakan dengan besarnya atau penjang vektor resultan dan arahnya sesuai dengan hasil dari gambar yang didapat, seperti vektor berikut ini
Gambarkan resultan vektor r yang merupakan jumlah dari vektor a, b dan c dengan cara menggambarkan vektor dari pangkal vektor a ke ujung vektor c, vektor resultan dinyatakan dengan besarnya atau penjang vektor resultan dan arahnya sesuai dengan hasil dari gambar yang didapat, seperti vektor berikut ini
|
b. Cara Segitiga
Untuk cara segitiga, berlaku untuk tiap-tiap dua vektor. Semua pangkal vektor-vektor yang akan dijumlahkan digabung menjadi satu titik tangkap. Kemudian gambarkan vektor resultan dengan menghubungkan kedua ujung vektor tersebut.
 | |||
c. Cara Jajaran Genjang
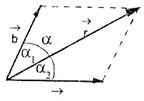
Untuk cara jajaran genjang, semua pangkal vektor-vektor yang akan dijumlahkan digabung menjadi satu titik tangkap. Kemudian gambarkan vektor bayangan masing-masing vektor. Selanjutnya gambarlah vektor resultan dari titik tangkap ke perpotongan vektor bayangan. Perhatikan contoh penjumlahan vektor secara jajaran genjang berikut ini.
 | |||
|
|
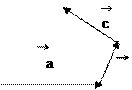
Untuk vektor yang lebih dari dua; pertama kali tentukan a + b terlebih dahulu, kemudian ( a + b ) + c, perhatikan contoh berikut ini.
 | |||
 | |||
| |||||
| |||||
|



|
|
|
2. Cara analitis.
Masing-masing vektor diuraikan menjadi komponen-komponen vektor searah sumbu x dan sumbu y dari sistem koordinat Cartesius.
Vektor
|
a
|
v x = v cos a
|
v y = v sin a
|
v1
v2
v3
|
a1
a2
a3
|
v1 x = v cos a1
v2 x = v cos a2
v3 x = v cos a3
|
v1 y = v sin a1
v2 y = v sin a2
v3 y = v sin a3
|
åv x = ................
|
åv y = ................
| ||
Menurut Bresnick besar Resultan vektor dan arah ditentukan dengan :
C. Vektor dalam Bidang Datar
Dengan mendefinisikan vektor satuan i dan j yang masing-masing searah sumbu X dan Y, untuk vektor dua dimensi akan berlaku r = x i + y j . Misalnya posisi titik A pada gambar 3 berikut ini.
|
|
|
|
|
|
Koordinat titik P(x, y, z) sebagai vektor tiga dimensi.
 |
j
Gambar 3. Vektor Dua dimensi Gambar 4. Vektor Tiga Dimensi
1. Resultan Vektor-vektor dalam Bidang Datar 2 Dimensi (x,y)
a. Segaris
b.Vektor yang membentuk sudut
Besar resultan vektor a dan b dirumuskan:
|
Batas besar resultan yang mungkin antara vektor a dan b adalah:
| a - b | < r < a + b
c. Pengurangan Vektor
|
a = sudut apit antara vektor a dan b
2. Menguraikan vektor menjadi komponen-komponen menurut sb. X dan sb. Y dalam satu bidang
 Suatu vektor
Suatu vektor
a = sudut apit antara v dan sumbu X positif
Apabila yang membentuk sudut terhadap sumbu X lebih dari satu vektor maka:
Contoh soal:
1. Dua buah vektor F1 = 5 N, F2 = 12 N membentuk sudut q = 600, maka tentukan resultan dari F1 + F2
Jawab :
|
 |
2. Tentukan besar komponen gaya sumbu X dan Y
Jawab
Fx = F cos q = 60 cos 60° = 60 x 0,5 = 30 N
3. Tentukan besar dan arah vektor yang memiliki komponen-komponen sebagai berikut :
a. Ax = 3 cm, Ay = 4 cm
Jawab:
a.
|
|
b.
|
Mengetahui: F1 = 40 N F2 = 60 N F3 = 30 N
Jawab:
Rx = F1 cos q° + F2 cos (120°) + F3 cos (240°)
= 40 . 1 + 60 . - 0,5 + 30 . – 0,5
= 40 - 30 – 15 = - 5
Ry = F1 sin q° + F2 sin (120°) + F3 sin (240°)
= 40 . 0 + 60 . 0,5 + 30 . – 0,5
= 0 + 30 – 15 = 15
|





Comments
Post a Comment
terima kasih telah berpartisipasi pada blog kami